321		231		132
Rectified 321			birectified 321
Rectified 231			Rectified 132
Orthogonal projections in E7 Coxeter plane

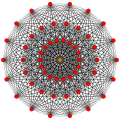
In 7-dimensional geometry, 2₃₁ is a uniform polytope, constructed from the E7 group.

Its Coxeter symbol is 2₃₁, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node branch.

The rectified 2₃₁ is constructed by points at the mid-edges of the 2₃₁.

These polytopes are part of a family of 127 (or 2⁷−1) convex uniform polytopes in 7-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: .

Gosset 231 polytope
Type	Uniform 7-polytope
Family	2k1 polytope
Schläfli symbol	{3,3,33,1}
Coxeter symbol	231
Coxeter diagram
6-faces	632: 56 221 576 {35}
5-faces	4788: 756 211 4032 {34}
4-faces	16128: 4032 201 12096 {33}
Cells	20160 {32}
Faces	10080 {3}
Edges	2016
Vertices	126
Vertex figure	131
Petrie polygon	Octadecagon
Coxeter group	E7, [33,2,1]
Properties	convex

The 2₃₁ is composed of 126 vertices, 2016 edges, 10080 faces (Triangles), 20160 cells (tetrahedra), 16128 4-faces (3-simplexes), 4788 5-faces (756 pentacrosses, and 4032 5-simplexes), 632 6-faces (576 6-simplexes and 56 2₂₁). Its vertex figure is a 6-demicube. Its 126 vertices represent the root vectors of the simple Lie group E₇.

This polytope is the vertex figure for a uniform tessellation of 7-dimensional space, 3₃₁.

• E. L. Elte named it V₁₂₆ (for its 126 vertices) in his 1912 listing of semiregular polytopes.^[1]
• It was called 2₃₁ by Coxeter for its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequence.
• Pentacontihexa-pentacosiheptacontihexa-exon (Acronym laq) - 56-576 facetted polyexon (Jonathan Bowers)^[2]

It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram, .

Removing the node on the short branch leaves the 6-simplex. There are 576 of these facets. These facets are centered on the locations of the vertices of the 3₂₁ polytope, .

Removing the node on the end of the 3-length branch leaves the 2₂₁. There are 56 of these facets. These facets are centered on the locations of the vertices of the 1₃₂ polytope, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 6-demicube, 1₃₁, .

Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.^[3]

E7		k-face	fk	f0	f1	f2	f3	f4		f5		f6		k-figures	notes
D6		( )	f0	126	32	240	640	160	480	60	192	12	32	6-demicube	E7/D6 = 72x8!/32/6! = 126
A5A1		{ }	f1	2	2016	15	60	20	60	15	30	6	6	rectified 5-simplex	E7/A5A1 = 72x8!/6!/2 = 2016
A3A2A1		{3}	f2	3	3	10080	8	4	12	6	8	4	2	tetrahedral prism	E7/A3A2A1 = 72x8!/4!/3!/2 = 10080
A3A2		{3,3}	f3	4	6	4	20160	1	3	3	3	3	1	tetrahedron	E7/A3A2 = 72x8!/4!/3! = 20160
A4A2		{3,3,3}	f4	5	10	10	5	4032	*	3	0	3	0	{3}	E7/A4A2 = 72x8!/5!/3! = 4032
A4A1				5	10	10	5	*	12096	1	2	2	1	Isosceles triangle	E7/A4A1 = 72x8!/5!/2 = 12096
D5A1		{3,3,3,4}	f5	10	40	80	80	16	16	756	*	2	0	{ }	E7/D5A1 = 72x8!/32/5! = 756
A5		{3,3,3,3}		6	15	20	15	0	6	*	4032	1	1		E7/A5 = 72x8!/6! = 72*8*7 = 4032
E6		{3,3,32,1}	f6	27	216	720	1080	216	432	27	72	56	*	( )	E7/E6 = 72x8!/72x6! = 8*7 = 56
A6		{3,3,3,3,3}		7	21	35	35	0	21	0	7	*	576		E7/A6 = 72x8!/7! = 72×8 = 576

Coxeter plane projections

E7	E6 / F4	B6 / A6
[18]	[12]	[7x2]
A5	D7 / B6	D6 / B5
[6]	[12/2]	[10]
D5 / B4 / A4	D4 / B3 / A2 / G2	D3 / B2 / A3
[8]	[6]	[4]

2k1 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8+	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8++
Coxeter diagram
Symmetry	[3−1,2,1]	[30,2,1]	[[31,2,1]]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2−1,1	201	211	221	231	241	251	261

Rectified 231 polytope
Type	Uniform 7-polytope
Family	2k1 polytope
Schläfli symbol	{3,3,33,1}
Coxeter symbol	t1(231)
Coxeter diagram
6-faces	758
5-faces	10332
4-faces	47880
Cells	100800
Faces	90720
Edges	30240
Vertices	2016
Vertex figure	6-demicube
Petrie polygon	Octadecagon
Coxeter group	E7, [33,2,1]
Properties	convex

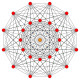
The rectified 2₃₁ is a rectification of the 2₃₁ polytope, creating new vertices on the center of edge of the 2₃₁.

• Rectified pentacontihexa-pentacosiheptacontihexa-exon - as a rectified 56-576 facetted polyexon (acronym rolaq) (Jonathan Bowers)^[4]

It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram, .

Removing the node on the short branch leaves the rectified 6-simplex, .

Removing the node on the end of the 2-length branch leaves the, 6-demicube, .

Removing the node on the end of the 3-length branch leaves the rectified 2₂₁, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node.

Coxeter plane projections

E7	E6 / F4	B6 / A6
[18]	[12]	[7x2]
A5	D7 / B6	D6 / B5
[6]	[12/2]	[10]
D5 / B4 / A4	D4 / B3 / A2 / G2	D3 / B2 / A3
[8]	[6]	[4]

• List of E7 polytopes

• Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
• H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Klitzing, Richard. "7D uniform polytopes (polyexa)". x3o3o3o *c3o3o3o - laq, o3x3o3o *c3o3o3o - rolaq