This article needs attention from an expert in statistics. The specific problem is: completion to reasonable standard for probability distributions. WikiProject Statistics may be able to help recruit an expert. (November 2012)

Johnson's S_U

Probability density function
Cumulative distribution function
Parameters	${\displaystyle \gamma ,\xi ,\delta >0,\lambda >0}$ (real)
Support	${\displaystyle -\infty {\text{ to }}+\infty }$
PDF	${\displaystyle {\frac {\delta }{\lambda {\sqrt {2\pi }}}}{\frac {1}{\sqrt {1+\left({\frac {x-\xi }{\lambda }}\right)^{2}}}}e^{-{\frac {1}{2}}\left(\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)\right)^{2}}}$
CDF	${\displaystyle \Phi \left(\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)\right)}$
Mean	${\displaystyle \xi -\lambda \exp {\frac {\delta ^{-2}}{2}}\sinh \left({\frac {\gamma }{\delta }}\right)}$
Median	${\displaystyle \xi +\lambda \sinh \left(-{\frac {\gamma }{\delta }}\right)}$
Variance	${\displaystyle {\frac {\lambda ^{2}}{2}}(\exp(\delta ^{-2})-1)\left(\exp(\delta ^{-2})\cosh \left({\frac {2\gamma }{\delta }}\right)+1\right)}$
Skewness	${\displaystyle -{\frac {\lambda ^{3}{\sqrt {e^{\delta ^{-2}}}}(e^{\delta ^{-2}}-1)^{2}((e^{\delta ^{-2}})(e^{\delta ^{-2}}+2)\sinh({\frac {3\gamma }{\delta }})+3\sinh({\frac {2\gamma }{\delta }}))}{4(\operatorname {Variance} X)^{1.5}}}}$
Excess kurtosis	${\displaystyle {\frac {\lambda ^{4}(e^{\delta ^{-2}}-1)^{2}(K_{1}+K_{2}+K_{3})}{8(\operatorname {Variance} X)^{2}}}}$ ${\displaystyle K_{1}=\left(e^{\delta ^{-2}}\right)^{2}\left(\left(e^{\delta ^{-2}}\right)^{4}+2\left(e^{\delta ^{-2}}\right)^{3}+3\left(e^{\delta ^{-2}}\right)^{2}-3\right)\cosh \left({\frac {4\gamma }{\delta }}\right)}$ ${\displaystyle K_{2}=4\left(e^{\delta ^{-2}}\right)^{2}\left(\left(e^{\delta ^{-2}}\right)+2\right)\cosh \left({\frac {3\gamma }{\delta }}\right)}$ ${\displaystyle K_{3}=3\left(2\left(e^{\delta ^{-2}}\right)+1\right)}$

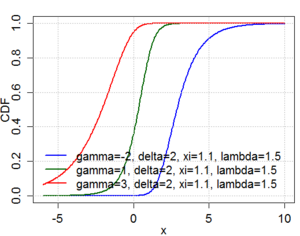
The Johnson's S_U-distribution is a four-parameter family of probability distributions first investigated by N. L. Johnson in 1949.^[1][2] Johnson proposed it as a transformation of the normal distribution:^[1]

${\displaystyle z=\gamma +\delta \sinh ^{-1}\left({\frac {x-\xi }{\lambda }}\right)}$

where ${\displaystyle z\sim {\mathcal {N}}(0,1)}$.

Let U be a random variable that is uniformly distributed on the unit interval [0, 1]. Johnson's S_U random variables can be generated from U as follows:

${\displaystyle x=\lambda \sinh \left({\frac {\Phi ^{-1}(U)-\gamma }{\delta }}\right)+\xi }$

where Φ is the cumulative distribution function of the normal distribution.

N. L. Johnson^[1] firstly proposes the transformation :

${\displaystyle z=\gamma +\delta \log \left({\frac {x-\xi }{\xi +\lambda -x}}\right)}$

where ${\displaystyle z\sim {\mathcal {N}}(0,1)}$.

Johnson's S_B random variables can be generated from U as follows:

${\displaystyle y={\left(1+{e}^{-\left(z-\gamma \right)/\delta }\right)}^{-1}}$

${\displaystyle x=\lambda y+\xi }$

The S_B-distribution is convenient to Platykurtic distributions (Kurtosis). To simulate S_U, sample of code for its density and cumulative distribution function is available here

Johnson's ${\displaystyle S_{U}}$-distribution has been used successfully to model asset returns for portfolio management.^[3] This comes as a superior alternative to using the Normal distribution to model asset returns. An R package, JSUparameters, was developed in 2021 to aid in the estimation of the parameters of the best-fitting Johnson's ${\displaystyle S_{U}}$-distribution for a given dataset. Johnson distributions are also sometimes used in option pricing, so as to accommodate an observed volatility smile; see Johnson binomial tree.

An alternative to the Johnson system of distributions is the quantile-parameterized distributions (QPDs). QPDs can provide greater shape flexibility than the Johnson system. Instead of fitting moments, QPDs are typically fit to empirical CDF data with linear least squares.

Johnson's ${\displaystyle S_{U}}$-distribution is also used in the modelling of the invariant mass of some heavy mesons in the field of B-physics.^[4]

• Hill, I. D.; Hill, R.; Holder, R. L. (1976). "Algorithm AS 99: Fitting Johnson Curves by Moments". Journal of the Royal Statistical Society. Series C (Applied Statistics). 25 (2).
• Jones, M. C.; Pewsey, A. (2009). "Sinh-arcsinh distributions" (PDF). Biometrika. 96 (4): 761. doi:10.1093/biomet/asp053.( Preprint)
• Tuenter, Hans J. H. (November 2001). "An algorithm to determine the parameters of S_U-curves in the Johnson system of probability distributions by moment matching". The Journal of Statistical Computation and Simulation. 70 (4): 325–347. doi:10.1080/00949650108812126. MR 1872992. Zbl 1098.62523.