|
Truncated pentahexagonal tiling
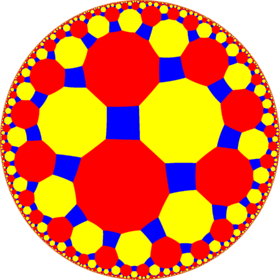
In geometry, the truncated tetrahexagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one decagon, and one dodecagon on each vertex. It has Schläfli symbol of t0,1,2{6,5}. Its name is somewhat misleading: literal geometric truncation of pentahexagonal tiling produces rectangles instead of squares. Dual tiling
SymmetryThere are four small index subgroup from [6,5] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
Related polyhedra and tilingsFrom a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-5 hexagonal tiling. Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are seven forms with full [6,5] symmetry, and three with subsymmetry.
See alsoReferences
External links |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||