|
Modèle d'EinsteinEn physique statistique et en physique du solide, le modèle d’Einstein est un modèle permettant de décrire la contribution des vibrations du réseau à la capacité calorifique d’un solide cristallin. Il repose sur les hypothèses suivantes :
Ce modèle est nommé d’après Albert Einstein, qui l'a proposé en 1907[1]. Énergie interneLes vibrations du réseau cristallin sont quantifiées[2], c’est-à-dire que les énergies de chaque mode normal de vibration ne peuvent prendre que des valeurs discrètes . Ce modèle repose donc sur la dualité onde-particule des phonons et sur le fait que les 3N oscillateurs harmoniques[3] vibrent à la même fréquence, de manière isotrope. L’énergie interne U du solide est donnée par la formule : où ℏ est la constante de Planck réduite, ωE est la pulsation d’un oscillateur, N le nombre d’atomes qui constituent le système et où kB est la constante de Boltzmann et T la température absolue. Démonstration de la formule de l’énergie interne
L’énergie d’un oscillateur harmonique à une dimension vibrant à la fréquence est donnée par : où est un nombre quantique On calcule la fonction de partition d’un oscillateur harmonique quantique qui est donnée par la relation : où kB est la constante de Boltzmann, T la température absolue et j est un état de l’oscillateur. Il y a un seul état par niveau d’énergie ; la somme devient donc : En appliquant la formule de la somme d’une suite géométrique, on simplifie la fonction de partition : On obtient alors l’énergie d’un oscillateur : avec ce qui donne On remarque au passage que . Cette énergie correspond à l’énergie de point zéro pour ne pas violer le principe d’incertitude d’Heisenberg[4]. On ne tient pas compte de l’énergie de point zéro ce qui donne L’énergie interne du système est alors : [5] Capacité calorifiqueLa capacité calorifique CV est définie par : avec , on obtient On peut définir la température d’Einstein comme . Tout cela nous donne Résultats du modèle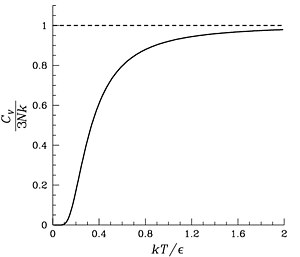 Le modèle d’Einstein retrouve la loi de Dulong et Petit, pour les hautes températures : Cependant, à basse température, ce modèle concorde moins avec les mesures expérimentales que celui de Debye : Lorsque Cette discordance avec l’expérience peut s’expliquer en abandonnant l’hypothèse selon laquelle les oscillateurs harmoniques vibrent à la même fréquence. Voir aussiArticles connexesBibliographie
Notes et références
Information related to Modèle d'Einstein |


















![{\displaystyle c_{V}\left(T\right)=3Nk_{B}\cdot \left({\frac {\Theta _{E}}{T}}\right)^{2}\cdot {\frac {\exp \left({\frac {\Theta _{E}}{T}}\right)}{\left[\exp \left({\frac {\Theta _{E}}{T}}\right)-1\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f71249b03764f9b233746dbd38f160d798d7db4)




