Hemi-icosahedron
decagonal Schlegel diagram
Type	abstract regular polyhedron globally projective polyhedron
Faces	10 triangles
Edges	15
Vertices	6
Euler char.	χ = 1
Vertex configuration	3.3.3.3.3
Schläfli symbol	{3,5}/2 or {3,5}5
Symmetry group	A5, order 60
Dual polyhedron	hemi-dodecahedron
Properties	non-orientable

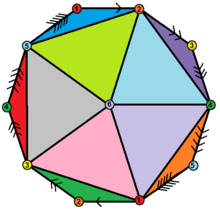
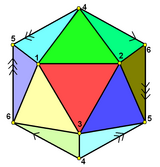
In geometry, a hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.

It has 10 triangular faces, 15 edges, and 6 vertices.

It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles.

It can be represented symmetrically on faces, and vertices as Schlegel diagrams:

Face-centered

It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces.

From the point of view of graph theory this is an embedding of ${\displaystyle K_{6}}$ (the complete graph with 6 vertices) on a real projective plane. With this embedding, the dual graph is the Petersen graph --- see hemi-dodecahedron.

• 11-cell - an abstract regular 4-polytope constructed from 11 hemi-icosahedra.
• hemi-dodecahedron
• hemi-cube
• hemi-octahedron

• McMullen, Peter; Schulte, Egon (December 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0

• The hemi-icosahedron