Order-5 cubic honeycomb
Poincaré disk models
Type	Hyperbolic regular honeycomb Uniform hyperbolic honeycomb
Schläfli symbol	{4,3,5}
Coxeter diagram
Cells	{4,3} (cube)
Faces	{4} (square)
Edge figure	{5} (pentagon)
Vertex figure	icosahedron
Coxeter group	BH3, [4,3,5]
Dual	Order-4 dodecahedral honeycomb
Properties	Regular

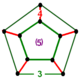
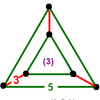
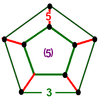
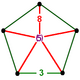
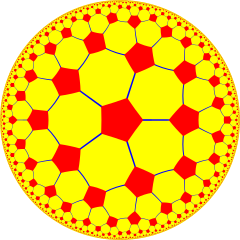
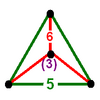
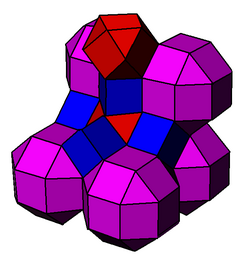
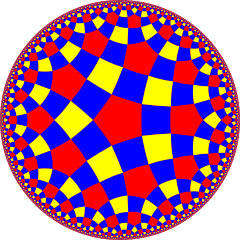
In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations (or honeycombs) in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

One cell, centered in Poincare ball model

Main cells

Cells with extended edges to ideal boundary

It has a radical subgroup symmetry construction with dodecahedral fundamental domains: Coxeter notation: [4,(3,5)^*], index 120.

The order-5 cubic honeycomb has a related alternated honeycomb, ↔ , with icosahedron and tetrahedron cells.

The honeycomb is also one of four regular compact honeycombs in 3D hyperbolic space:

Four regular compact honeycombs in H³

{5,3,4}

{4,3,5}

{3,5,3}

{5,3,5}

There are fifteen uniform honeycombs in the [5,3,4] Coxeter group family, including the order-5 cubic honeycomb as the regular form:

[5,3,4] family honeycombs

{5,3,4}	r{5,3,4}	t{5,3,4}	rr{5,3,4}	t0,3{5,3,4}	tr{5,3,4}	t0,1,3{5,3,4}	t0,1,2,3{5,3,4}
{4,3,5}	r{4,3,5}	t{4,3,5}	rr{4,3,5}	2t{4,3,5}	tr{4,3,5}	t0,1,3{4,3,5}	t0,1,2,3{4,3,5}

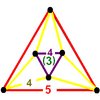
The order-5 cubic honeycomb is in a sequence of regular polychora and honeycombs with icosahedral vertex figures.

{p,3,5} polytopes
Space	S3	H3
Form	Finite	Compact		Paracompact	Noncompact
Name	{3,3,5}	{4,3,5}	{5,3,5}	{6,3,5}	{7,3,5}	{8,3,5}	... {∞,3,5}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

It is also in a sequence of regular polychora and honeycombs with cubic cells. The first polytope in the sequence is the tesseract, and the second is the Euclidean cubic honeycomb.

{4,3,p} regular honeycombs
Space	S3	E3	H3
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Rectified order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	r{4,3,5} or 2r{5,3,4} 2r{5,31,1}
Coxeter diagram	↔
Cells	r{4,3} {3,5}
Faces	triangle {3} square {4}
Vertex figure	pentagonal prism
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5] ${\displaystyle {\overline {DH}}_{3}}$, [5,31,1]
Properties	Vertex-transitive, edge-transitive

The rectified order-5 cubic honeycomb, , has alternating icosahedron and cuboctahedron cells, with a pentagonal prism vertex figure.

There are four rectified compact regular honeycombs:

Four rectified regular compact honeycombs in H³

Image
Symbols	r{5,3,4}	r{4,3,5}	r{3,5,3}	r{5,3,5}
Vertex figure

r{p,3,5}

Space	S3	H3
Form	Finite	Compact		Paracompact	Noncompact
Name	r{3,3,5}	r{4,3,5}	r{5,3,5}	r{6,3,5}	r{7,3,5}	... r{∞,3,5}
Image
Cells {3,5}	r{3,3}	r{4,3}	r{5,3}	r{6,3}	r{7,3}	r{∞,3}

Truncated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t{4,3,5}
Coxeter diagram
Cells	t{4,3} {3,5}
Faces	triangle {3} octagon {8}
Vertex figure	pentagonal pyramid
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The truncated order-5 cubic honeycomb, , has truncated cube and icosahedron cells, with a pentagonal pyramid vertex figure.

It can be seen as analogous to the 2D hyperbolic truncated order-5 square tiling, t{4,5}, with truncated square and pentagonal faces:

It is similar to the Euclidean (order-4) truncated cubic honeycomb, t{4,3,4}, which has octahedral cells at the truncated vertices.

Four truncated regular compact honeycombs in H³

Image
Symbols	t{5,3,4}	t{4,3,5}	t{3,5,3}	t{5,3,5}
Vertex figure

The bitruncated order-5 cubic honeycomb is the same as the bitruncated order-4 dodecahedral honeycomb.

Cantellated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	rr{4,3,5}
Coxeter diagram
Cells	rr{4,3} r{3,5} {}x{5}
Faces	triangle {3} square {4} pentagon {5}
Vertex figure	wedge
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The cantellated order-5 cubic honeycomb, , has rhombicuboctahedron, icosidodecahedron, and pentagonal prism cells, with a wedge vertex figure.

It is similar to the Euclidean (order-4) cantellated cubic honeycomb, rr{4,3,4}:

Four cantellated regular compact honeycombs in H3
Image Symbols rr{5,3,4} rr{4,3,5} rr{3,5,3} rr{5,3,5} Vertex figure

Cantitruncated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	tr{4,3,5}
Coxeter diagram
Cells	tr{4,3} t{3,5} {}x{5}
Faces	square {4} pentagon {5} hexagon {6} octagon {8}
Vertex figure	mirrored sphenoid
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The cantitruncated order-5 cubic honeycomb, , has truncated cuboctahedron, truncated icosahedron, and pentagonal prism cells, with a mirrored sphenoid vertex figure.

It is similar to the Euclidean (order-4) cantitruncated cubic honeycomb, tr{4,3,4}:

Four cantitruncated regular compact honeycombs in H³

Image
Symbols	tr{5,3,4}	tr{4,3,5}	tr{3,5,3}	tr{5,3,5}
Vertex figure

Runcinated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space Semiregular honeycomb
Schläfli symbol	t0,3{4,3,5}
Coxeter diagram
Cells	{4,3} {5,3} {}x{5}
Faces	square {4} pentagon {5}
Vertex figure	irregular triangular antiprism
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The runcinated order-5 cubic honeycomb or runcinated order-4 dodecahedral honeycomb , has cube, dodecahedron, and pentagonal prism cells, with an irregular triangular antiprism vertex figure.

It is analogous to the 2D hyperbolic rhombitetrapentagonal tiling, rr{4,5}, with square and pentagonal faces:

It is similar to the Euclidean (order-4) runcinated cubic honeycomb, t_0,3{4,3,4}:

Three runcinated regular compact honeycombs in H³

Image
Symbols	t0,3{4,3,5}	t0,3{3,5,3}	t0,3{5,3,5}
Vertex figure

Runctruncated order-5 cubic honeycomb Runcicantellated order-4 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,1,3{4,3,5}
Coxeter diagram
Cells	t{4,3} rr{5,3} {}x{5} {}x{8}
Faces	triangle {3} square {4} pentagon {5} octagon {8}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The runcitruncated order-5 cubic honeycomb or runcicantellated order-4 dodecahedral honeycomb, , has truncated cube, rhombicosidodecahedron, pentagonal prism, and octagonal prism cells, with an isosceles-trapezoidal pyramid vertex figure.

It is similar to the Euclidean (order-4) runcitruncated cubic honeycomb, t_0,1,3{4,3,4}:

Four runcitruncated regular compact honeycombs in H3
Image Symbols t0,1,3{5,3,4} t0,1,3{4,3,5} t0,1,3{3,5,3} t0,1,3{5,3,5} Vertex figure

The runcicantellated order-5 cubic honeycomb is the same as the runcitruncated order-4 dodecahedral honeycomb.

Omnitruncated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space Semiregular honeycomb
Schläfli symbol	t0,1,2,3{4,3,5}
Coxeter diagram
Cells	tr{5,3} tr{4,3} {10}x{} {8}x{}
Faces	square {4} hexagon {6} octagon {8} decagon {10}
Vertex figure	irregular tetrahedron
Coxeter group	${\displaystyle {\overline {BH}}_{3}}$, [4,3,5]
Properties	Vertex-transitive

The omnitruncated order-5 cubic honeycomb or omnitruncated order-4 dodecahedral honeycomb, , has truncated icosidodecahedron, truncated cuboctahedron, decagonal prism, and octagonal prism cells, with an irregular tetrahedral vertex figure.

It is similar to the Euclidean (order-4) omnitruncated cubic honeycomb, t_0,1,2,3{4,3,4}:

Three omnitruncated regular compact honeycombs in H3
Image Symbols t0,1,2,3{4,3,5} t0,1,2,3{3,5,3} t0,1,2,3{5,3,5} Vertex figure

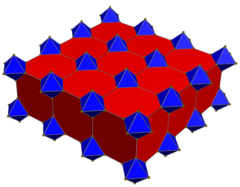
Alternated order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	h{4,3,5}
Coxeter diagram	↔
Cells	{3,3} {3,5}
Faces	triangle {3}
Vertex figure	icosidodecahedron
Coxeter group	${\displaystyle {\overline {DH}}_{3}}$, [5,31,1]
Properties	Vertex-transitive, edge-transitive, quasiregular

In 3-dimensional hyperbolic geometry, the alternated order-5 cubic honeycomb is a uniform compact space-filling tessellation (or honeycomb). With Schläfli symbol h{4,3,5}, it can be considered a quasiregular honeycomb, alternating icosahedra and tetrahedra around each vertex in an icosidodecahedron vertex figure.

It has 3 related forms: the cantic order-5 cubic honeycomb, , the runcic order-5 cubic honeycomb, , and the runcicantic order-5 cubic honeycomb, .

Cantic order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	h2{4,3,5}
Coxeter diagram	↔
Cells	r{5,3} t{3,5} t{3,3}
Faces	triangle {3} pentagon {5} hexagon {6}
Vertex figure	rectangular pyramid
Coxeter group	${\displaystyle {\overline {DH}}_{3}}$, [5,31,1]
Properties	Vertex-transitive

The cantic order-5 cubic honeycomb is a uniform compact space-filling tessellation (or honeycomb), with Schläfli symbol h₂{4,3,5}. It has icosidodecahedron, truncated icosahedron, and truncated tetrahedron cells, with a rectangular pyramid vertex figure.

Runcic order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	h3{4,3,5}
Coxeter diagram	↔
Cells	{5,3} rr{5,3} {3,3}
Faces	triangle {3} square {4} pentagon {5}
Vertex figure	triangular frustum
Coxeter group	${\displaystyle {\overline {DH}}_{3}}$, [5,31,1]
Properties	Vertex-transitive

The runcic order-5 cubic honeycomb is a uniform compact space-filling tessellation (or honeycomb), with Schläfli symbol h₃{4,3,5}. It has dodecahedron, rhombicosidodecahedron, and tetrahedron cells, with a triangular frustum vertex figure.

Runcicantic order-5 cubic honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	h2,3{4,3,5}
Coxeter diagram	↔
Cells	t{5,3} tr{5,3} t{3,3}
Faces	triangle {3} square {4} hexagon {6} decagon {10}
Vertex figure	irregular tetrahedron
Coxeter group	${\displaystyle {\overline {DH}}_{3}}$, [5,31,1]
Properties	Vertex-transitive

The runcicantic order-5 cubic honeycomb is a uniform compact space-filling tessellation (or honeycomb), with Schläfli symbol h_2,3{4,3,5}. It has truncated dodecahedron, truncated icosidodecahedron, and truncated tetrahedron cells, with an irregular tetrahedron vertex figure.

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II, III, IV, V, p212-213)
• Norman Johnson Uniform Polytopes, Manuscript
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • N.W. Johnson: Geometries and Transformations, (2015) Chapter 13: Hyperbolic Coxeter groups