Loi de Delaporte

Loi de Delaporte
Fonction de masse
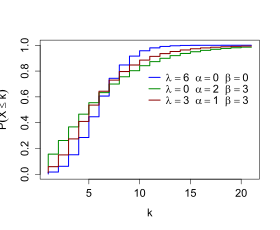
Fonction de répartition
Paramètres	${\displaystyle \lambda >0}$ ${\displaystyle \alpha ,\beta >0}$
Support	${\displaystyle k\in \{0,1,2,\ldots \}}$
Fonction de masse	${\displaystyle \sum _{i=0}^{k}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{k-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(k-i)!}}}$
Fonction de répartition	${\displaystyle \sum _{j=0}^{k}\sum _{i=0}^{j}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{j-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(j-i)!}}}$
Espérance	${\displaystyle \lambda +\alpha \beta }$
Mode	voir l'article
Variance	${\displaystyle \lambda +\alpha \beta (1+\beta )}$
Asymétrie	voir l'article
Kurtosis normalisé	voir l'article
modifier

En théorie des probabilités et en statistique, la loi de Delaporte est une loi de probabilité discrète qui est particulièrement utilisée en science actuarielle^[1],[2]. Cette loi est la convolution d'une loi binomiale négative avec une loi de Poisson^[2]. Puisque la loi binomiale négative peut être vue comme une loi de Poisson dont le paramètre de moyenne est lui-même une variable aléatoire de loi gamma, la loi de Delaporte peut être vue comme une loi composée d'une loi de Poisson où le paramètre de moyenne se décompose en deux composants : un composant fixe de paramètre ${\displaystyle \lambda }$, et un composant de loi gamma de paramètres ${\displaystyle \alpha }$ et ${\displaystyle \beta }$^[3].

Le nom de cette loi est issue de Pierre Delaporte qui proposa une relation avec le comptage des accidents de voitures en 1959^[4], bien qu'elle apparaisse plus tôt sous différentes formes en 1934 dans un article de Rolf von Lüders^[5] où la loi est appelée formulation II (Formel II distribution en allemand).

Le mode de la loi de Delaporte est donnée par :

${\displaystyle {\begin{cases}z\ \mathrm {ou} \ z+1&{\text{, si }}z{\text{ est l'entier }}z=(\alpha -1)\beta +\lambda \\\lfloor z\rfloor &{\textrm {,}}\ {\textrm {sinon.}}\end{cases}}}$

L'asymétrie de la loi de Delaporte est donnée par :

${\displaystyle \gamma _{1}={\frac {\lambda +\alpha \beta (1+3\beta +2\beta ^{2})}{\left[\lambda +\alpha \beta (1+\beta )\right]^{\frac {3}{2}}}}.}$

Le kurtosis de la loi de Delaporte est donnée par :

${\displaystyle \gamma _{2}={\frac {\lambda +3\lambda ^{2}+\alpha \beta (1+6\lambda +6\lambda \beta +7\beta +12\beta ^{2}+6\beta ^{3}+3\alpha \beta +6\alpha \beta ^{2}+3\alpha \beta ^{3})}{\left[\lambda +\alpha \beta (1+\beta )\right]^{2}}}.}$

• Si ${\displaystyle \alpha =\beta =0}$, alors la loi de Delaporte est la loi de Poisson de paramètre ${\displaystyle \lambda }$.
• Si ${\displaystyle \lambda =0}$, alors la loi de Delaporte est la loi binomiale négative.

• (en) M. Murat et D. Szynal, « On moments of counting distributions satisfying the k'th-order recursion and their compound distributions », Journal of Mathematical Sciences, vol. 92, n^o 4,‎ 1998, p. 4038–4043 (DOI 10.1007/BF02432340)

• Portail des probabilités et de la statistique