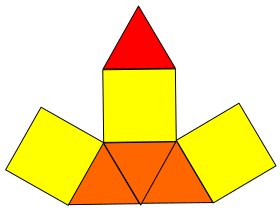
Elongated triangular pyramid
Type	Johnson J6 – J7 – J8
Faces	4 triangles 3 squares
Edges	12
Vertices	7
Vertex configuration	1(33) 3(3.42) 3(32.42)
Symmetry group	C3v, [3], (*33)
Rotation group	C3, [3]+, (33)
Dual polyhedron	self
Properties	convex
Net

In geometry, the elongated triangular pyramid is one of the Johnson solids (J₇). As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically (but not geometrically) self-dual.

The elongated triangular pyramid is constructed from a triangular prism by attaching regular tetrahedron onto one of its bases, a process known as elongation.^[1] The tetrahedron covers an equilateral triangle, replacing it with three other equilateral triangles, so that the resulting polyhedron has four equilateral triangles and three squares as its faces.^[2] A convex polyhedron in which all of the faces are regular polygons is called the Johnson solid, and the elongated triangular pyramid is among them, enumerated as the seventh Johnson solid ${\displaystyle J_{7}}$.^[3]

An elongated triangular pyramid with edge length ${\displaystyle a}$ has a height, by adding the height of a regular tetrahedron and a triangular prism:^[4] $${\displaystyle \left(1+{\frac {\sqrt {6}}{3}}\right)a\approx 1.816a.}$$ Its surface area can be calculated by adding the area of all eight equilateral triangles and three squares:^[2] $${\displaystyle \left(3+{\sqrt {3}}\right)a^{2}\approx 4.732a^{2},}$$ and its volume can be calculated by slicing it into a regular tetrahedron and a prism, adding their volume up:^[2]: $${\displaystyle \left({\frac {1}{12}}\left({\sqrt {2}}+3{\sqrt {3}}\right)\right)a^{3}\approx 0.551a^{3}.}$$

It has the three-dimensional symmetry group, the cyclic group ${\displaystyle C_{3\mathrm {v} }}$ of order 6. Its dihedral angle can be calculated by adding the angle of the tetrahedron and the triangular prism:^[5]

• the dihedral angle of a tetrahedron between two adjacent triangular faces is ${\textstyle \arccos \left({\frac {1}{3}}\right)\approx 70.5^{\circ }}$;
• the dihedral angle of the triangular prism between the square to its bases is ${\textstyle {\frac {\pi }{2}}=90^{\circ }}$, and the dihedral angle between square-to-triangle, on the edge where tetrahedron and triangular prism are attached, is ${\textstyle \arccos \left({\frac {1}{3}}\right)+{\frac {\pi }{2}}\approx 160.5^{\circ }}$;
• the dihedral angle of the triangular prism between two adjacent square faces is the internal angle of an equilateral triangle ${\textstyle {\frac {\pi }{3}}=60^{\circ }}$.

• Weisstein, Eric W., "Johnson solid" ("Elongated triangular pyramid") at MathWorld.