Tridiminished icosahedron
Type	Johnson J62 – J63 – J64
Faces	5 triangles 3 pentagons
Edges	15
Vertices	9
Vertex configuration	${\displaystyle 2\times 3\times (3\times 5^{2})+3\times (3^{3}\times 5)}$
Symmetry group	${\displaystyle C_{3\mathrm {v} }}$
Properties	convex, non-composite
Net

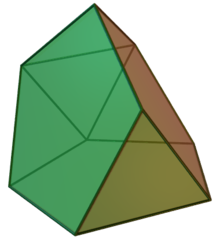
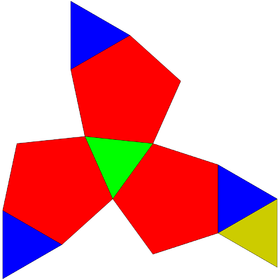
In geometry, the tridiminished icosahedron is a Johnson solid that is constructed by removing three pentagonal pyramids from a regular icosahedron.

The tridiminished icosahedron can be constructed by removing three regular pentagonal pyramid from a regular icosahedron.^[1] The aftereffect of such construction leaves five equilateral triangles and three regular pentagons.^[2] Since all of its faces are regular polygons and the resulting polyhedron remains convex, the tridiminished icosahedron is a Johnson solid, and it is enumerated as the sixty-third Johnson solid ${\displaystyle J_{63}}$.^[3] This construction is similar to other Johnson solids as in gyroelongated pentagonal pyramid and metabidiminished icosahedron.^[1]

The tridiminished icosahedron is non-composite polyhedron, meaning it is convex polyhedron that cannot be separated by a plane into two or more regular polyhedrons.^[4]

The surface area of a tridiminished icosahedron ${\displaystyle A}$ is the sum of all polygonal faces' area: five equilateral triangles and three regular pentagons. Its volume ${\displaystyle V}$ can be ascertained by subtracting the volume of a regular icosahedron with the volume of three pentagonal pyramids. Given that ${\displaystyle a}$ is the edge length of a tridiminished icosahedron, they are:^[2] $${\displaystyle {\begin{aligned}A&={\frac {5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}}{4}}a^{2}&\approx 7.3265a^{2},\\V&={\frac {15+7{\sqrt {5}}}{24}}a^{3}&\approx 1.2772a^{3}.\end{aligned}}}$$

• Snub 24-cell, a 4-polytope whose vertex figure is a tridiminished icosahedron

• Weisstein, Eric W., "Tridiminished icosahedron" ("Johnson Solid") at MathWorld.